อัตราผลตอบแทนที่ได้รับจริง (realized return) เป็นอัตราผลตอบแทนเพื่อแสดงว่าในการลงทุนที่ผ่านมานั้น ได้รับผลตอบแทนจริงจากการลงทุนมากน้อยเพียงใด
สามารถคำนวณได้จาก
อัตราผลตอบแทนที่ได้รับจริง = (มูลค่าปลายงวด - มูลค่าต้นงวด + เงินสดที่ได้รับระหว่างงวด) / มูลค่าต้นงวด
อัตราผลตอบแทนโดยเฉลี่ย (average rate of return) เป็นการคำนวณหาอัตราผลตอบแทนจากข้อมูลในอดีต
มีวิธีคำนวณอัตราผลตอบแทนโดยเฉลี่ยอยู่ 2 แบบ คือ
อัตราผลตอบแทน เฉลี่ยเลขคณิต (arithmetic average rate of return) คือ การนำอัตราผลตอบแทนมารวมกันทุกงวด แล้ว หารด้วย จำนวนงวด
อัตราผลตอบแทน เฉลี่ยเรขาคณิต คือ (geometric average rate of return) คือ การนำหลักการของดอกเบี้ยทบต้นมาใช้แล้วจึงหาค่าเฉลี่ย ทำให้มีสูตรการคำนวณที่ยากกว่า อัตราผลตอบแทน เฉลี่ยเลขคณิต
ตัวอย่างเช่น ผู้ลงทุนได้รับอัตราผลตอบแทนในปีที่ 1 เท่ากับ 10% และได้รับอัตราผลตอบแทนในปีที่ 2 เท่ากับ 20%
นักวางแผนการเงินควรคำนวณ อัตราผลตอบแทนเฉลี่ยเลขคณิต และ เรขาคณิต ได้
วิธีคำนวณสามารถดูได้จาก Video Clip ต่อไปนี้
ข้อสังเกต
อัตราผลตอบแทนเฉลี่ยเลขคณิตนั้นจะประเมินอัตราผลตอบแทนสูงกว่าความเป็นจริงอยู่เล็กน้อยเมื่อใช้กับข้อมูลที่มีคาบเวลายาวนานและโดยเฉพาะหลักทรัพย์ที่มีความผันผวนสูง
อัตราผลตอบแทนที่คาดหวัง (expected return)
เป็นการคาดการณ์อนาคตว่าการลงทุนในหลักทรัพย์น่าจะให้ผลตอบแทนเท่าใด
คำนวณได้จากค่าเฉลี่ยถ่วงน้ำหนักของอัตราผลตอบแทนที่เป็นไปได้ โดยน้ำหนักที่ถ่วง ได้แก่ ความน่าจะเป็น (probability) ที่จะเกิดอัตราผลตอบแทนที่เป็นไปได้
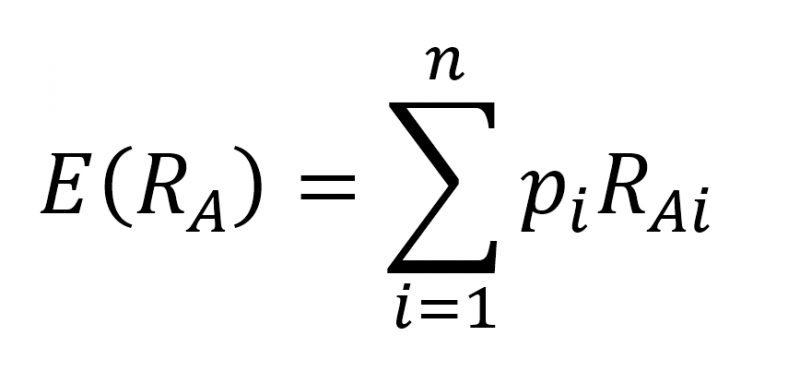
โดย
E(RA) = อัตราผลตอบแทนที่คาดหวังของหลักทรัพย์ A
RAi = อัตราผลตอบแทนที่เป็นไปได้ตามเหตุการณ์ที่ i
pi = ความน่าจะเป็นที่จะเกิดเหตุการณ์ที่ i โดยมีเหตุการณ์ทั้งสิ้น n เหตุการณ์ ที่เป็น Mutual Exclusive
ข้อพึงระวังคือ อัตราผลตอบแทนที่ได้รับจริง อาจจะมีค่าแตกต่างไปจากอัตราผลตอบแทนที่คาดหวัง ซึ่งมีผลมาจากความไม่แน่นอนที่เกิดจากปัจจัยต่างๆ
ความเสี่ยงจากการลงทุน
หมายถึงความไม่แน่นอนในการได้รับเงินคืนและได้รับผลตอบแทนจากการลงทุนตามที่คาดหวัง
ค่าความแปรปรวน และ ส่วนเบี่ยงเบนมาตรฐาน
เป็นวิธีทางสถิติในการวัดความเสี่ยงของราคาหลักทรัพย์ ค่าความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานที่มากขึ้น แสดงถึงระดับความผันผวน หรือความเสี่ยงที่มากขึ้น
ค่าความแปรปรวน คำนวณได้จาก
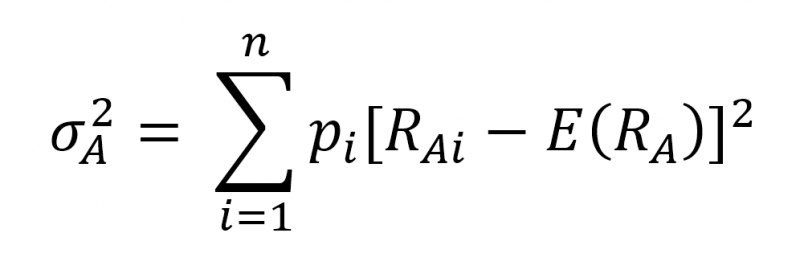
โดย pi คือ ความน่าจะเป็นที่จะเกิดเหตุการณ์ i
RAi = อัตราผลตอบแทนที่เป็นไปได้ตามเหตุการณ์ที่ i
E(RA) คืออัตราผลตอบแทนที่คาดไว้ของเหตุการณ์ i
และส่วนเบี่ยงเบนมาตรฐานคำนวณได้จาก
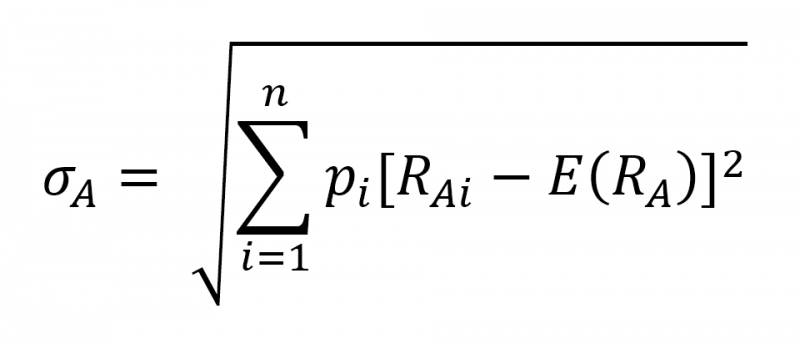
สังเกตได้ว่า ส่วนเบี่ยงเบนมาตรฐานสามารถคำนวณได้จาก รากที่ 2 ของ ความแปรปรวน
การคำนวณ อัตราผลตอบแทนที่คาดหวังและส่วนเบี่ยงเบนมาตรฐาน สามารถใช้เครื่องคิดเลขคำนวณได้ตาม Video Clip ต่อไปนี้
ค่าความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานจากอัตราผลตอบแทนในอดีต
ในบางกรณีข้อมูลที่มีไม่ใช่ความน่าจะเป็นที่จะเกิดแต่ละเหตุการณ์
คือ pi ไม่ได้กำหนดมาให้
แต่ให้อัตราผลตอบแทนในอดีตที่เกิดขึ้นจริงมาหลายๆงวด
แล้วให้คำนวณค่าความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน
สูตรคำนวณจะแตกต่างจากการคำนวณความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานเมื่อการมีการคาดการณ์ความน่าจะเป็น pi
ค่าความแปรปรวนคำนวณได้จาก
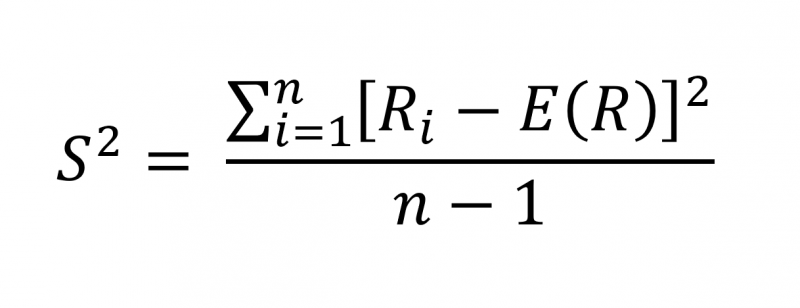
โดย Ri คือ ตัวอย่างอัตราผลตอบแทนในอดีต
E(R) คือ อัตราผลตอบแทนเฉลี่ยแบบเลขคณิต
และ ส่วนเบี่ยงเบนมาตรฐานสามารถคำนวณได้จากรากที่ 2 ของ ค่าความแปรปรวน
การคำนวณส่วนเบี่ยงเบนมาตรฐานนั้น สามารถใช้ เครื่องคิดเลขทางการเงินคำนวณได้ดังตัวอย่างต่อไปนี้
ตัวอย่างที่ 1-5 หน้า 22
อัตราผลตอบแทนที่ได้รับรายปีของหลักทรัพย์ตัวหนึ่ง ในช่วง 5 ปี หลังสุดคือ 30%, 12%, 25%, 20%, และ 23% ตามลำดับ จงคำนวณส่วนเบี่ยงเบนมาตรฐาน
วิธีคำนวณแสดงไว้ใน Clip ต่อไปนี้
เรียบเรียงจาก หนังสือ หลักสูตรวางแผนการเงิน : ชุดวิชาที่ 2 การวางแผนการลงทน
หัวข้อ 1.2
โดย ดร.ชาติชาย มีสุขโข CFP®

